The tangents at and to the circumcircle of the acute-angled triangle meet at . Let be the midpoint of . Prove that
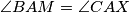
(a) , and
(b)
%V0
The tangents at $B$ and $C$ to the circumcircle of the acute-angled triangle $ABC$ meet at $X$. Let $M$ be the midpoint of $BC$. Prove that
(a) $\angle BAM = \angle CAX$, and
(b) $\frac{AM}{AX} = \cos\angle BAC.$
Izvor: Međunarodna matematička olimpijada, shortlist 1985
Školjka 
and 
to the circumcircle of the acute-angled triangle 
meet at 
. Let 
be the midpoint of 
. Prove that
, and