Vrijeme: 18:06
Skupovi i loptice #4
Imamo  skupova loptica označenih brojevima
skupova loptica označenih brojevima 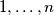 , koji ukupno sadrže
, koji ukupno sadrže  loptica. Želimo ih obojati u crveno ili plavo tako da su sve lopte s istom oznakom iste boje te da za svaki podskup od
loptica. Želimo ih obojati u crveno ili plavo tako da su sve lopte s istom oznakom iste boje te da za svaki podskup od 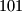 loptice s (ne nužno različitim) oznakama
loptice s (ne nužno različitim) oznakama 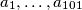 za koji vrijedi
za koji vrijedi 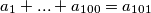 , vrijedi da nisu sve lopte u tom skupu iste boje. Koji je najveći
, vrijedi da nisu sve lopte u tom skupu iste boje. Koji je najveći  za koji je ovo moguće postići?
za koji je ovo moguće postići?
 skupova loptica označenih brojevima
skupova loptica označenih brojevima 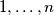 , koji ukupno sadrže
, koji ukupno sadrže  loptica. Želimo ih obojati u crveno ili plavo tako da su sve lopte s istom oznakom iste boje te da za svaki podskup od
loptica. Želimo ih obojati u crveno ili plavo tako da su sve lopte s istom oznakom iste boje te da za svaki podskup od 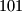 loptice s (ne nužno različitim) oznakama
loptice s (ne nužno različitim) oznakama 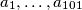 za koji vrijedi
za koji vrijedi 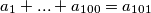 , vrijedi da nisu sve lopte u tom skupu iste boje. Koji je najveći
, vrijedi da nisu sve lopte u tom skupu iste boje. Koji je najveći  za koji je ovo moguće postići?
za koji je ovo moguće postići? 