Što je Školjka?
Školjka je web arhiva zadataka iz matematike, pomoćni alat i sredstvo motivacije namijenjen učenicima i studentima pri pripremi za natjecanja. Sadrži tisuće i tisuće zadataka s raznih matematičkih natjecanja u prethodnih dvadesetak godina te se redovito nadopunjava novim zadacima i natjecanjima.
Why Školjka?
Osim što služi kao baza zadataka, Školjka omogućuje pretraživanje istih po kategorijama i po težini. Učenici tako mogu jednostavno pronaći zadatke točno onog tipa koji ih zanima. Također, Školjka može biti od velike pomoći njihovim mentorima pri organizaciji priprema i predavanja.
Odabrana natjecanja
Nedavno objavljeni zadaci
Odredi proste brojeve $p,q,r$ i prirodni broj $n$ za koje vrijedi
\[p^2=q^2+r^n.\]
Nađi sva rješenja.
1 godina, 4 mjeseci
Odredi sve uređene parove $(p,n)$, pri čemu je $p$ prost, a $n$ prirodan broj za koje vrijedi
\[
1+p+p^{2}+p^{3}+ \dotsb +p^{n}=2801.
\]
1 godina, 4 mjeseci
Nedavne aktivnosti:
12. ožujka
19:38
FranJ je označio kao riješen zadatak
17:38
IvanK je označio kao riješen zadatak
16:14
FranJ je označio kao riješen zadatak
11. ožujka
18:46
FranJ je označio kao riješen zadatak
11:30
FranJ je označio kao riješen zadatak
11:19
FranJ je označio kao riješen zadatak
10. ožujka
23:35
IvanK je označio kao riješen zadatak
22:27
FranJ je označio kao riješen zadatak
22:05
FranJ je označio kao riješen zadatak
21:50
IvanK je označio kao riješen zadatak
21:18
FranJ je označio kao riješen zadatak
20:50
FranJ je označio kao riješen zadatak
07:55
FranJ je označio kao riješen zadatak
5. ožujka
13:48
IvanK je označio kao riješen zadatak
13:42
IvanK je označio kao riješen zadatak
13:36
IvanK je označio kao riješen zadatak
4. ožujka
23:34
IvanK je označio kao riješen zadatak
23:14
IvanK je označio kao riješen zadatak
3. ožujka
22:29
IvanK je označio kao riješen zadatak
14:26
IvanK je označio kao riješen zadatak
13:03
IvanK je označio kao riješen zadatak
12:52
IvanK je označio kao riješen zadatak
12:35
IvanK je označio kao riješen zadatak
12:18
IvanK je označio kao riješen zadatak
12:06
IvanK je označio kao riješen zadatak
08:35
FranJ je označio kao riješen zadatak
2. ožujka
22:12
IvanK je označio kao riješen zadatak
21:42
IvanK je označio kao riješen zadatak
21:29
IvanK je označio kao riješen zadatak
 Školjka
Školjka 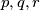 i prirodni broj
i prirodni broj  za koje vrijedi
za koje vrijedi 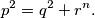 Nađi sva rješenja.
Nađi sva rješenja. 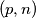 , pri čemu je
, pri čemu je  prost, a
prost, a