Odredite najmanji pozitivan realan broj

takav da ako vrijedi
![a_i \in \left[ 0, \frac{1}{2} \right]](/media/m/9/2/c/92c70c85a16aac722ec91f4d4ace36a0.png)
,
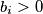
(
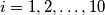
) i
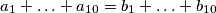
, da je tada

Rezultat napišite u obliku potpuno skraćenog razloma, koristeći "/" kao razlomačku crtu. (Npr. 1234/56789 )
%V0
Odredite najmanji pozitivan realan broj $k$ takav da ako vrijedi $a_i \in \left[ 0, \frac{1}{2} \right]$ , $b_i > 0$ ($i = 1, 2, \ldots, 10$) i $a_1 + \ldots + a_{10} = b_1 + \ldots + b_{10}$, da je tada $$
b_1 \cdot b_2 \cdots b_{10} \le k(a_1b_1 + \ldots + a_{10}b_{10}) \text{.}
$$
Rezultat napišite u obliku potpuno skraćenog razloma, koristeći "/" kao razlomačku crtu. (Npr. 1234/56789 )