Za koji
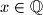
,

se postiže minimum izraza

uz uvjet da jednadžba
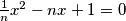
nema realne nultočke? Rješenje zapišite kao uređen par
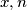
, gdje je

razlomak, a

cijeli broj.
%V0
Za koji $x \in \mathbb{Q}$, $n \in \mathbb{N}$ se postiže minimum izraza $ \frac{1}{n}x^2-nx+1$ uz uvjet da jednadžba $ \frac{1}{n}x^2-nx+1=0$ nema realne nultočke? Rješenje zapišite kao uređen par $x, n$, gdje je $x$ razlomak, a $n$ cijeli broj.