Za
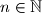
, neka je

broj dobiven zapisivanjem

u bazi

i zamijenom nula sa jedinicama i obrnuto. Npr.
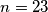
je u binarnom zapisu
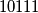
pa je
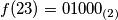
, odnosno
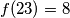
.
Odredi

za
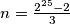
%V0
Za $n\in \mathbb{N}$, neka je $f(n)$ broj dobiven zapisivanjem $n$ u bazi $2$ i zamijenom nula sa jedinicama i obrnuto. Npr. $n=23$ je u binarnom zapisu $10111$ pa je $f(23)=01000_{(2)}$, odnosno $f(23)=8$.
Odredi $\sum_{k=1}^{n} f(k)$ za $n=\frac{2^{25}-2}{3} $