Vrijeme: 17:55
jedan lagani #5
Odgovorite u obliku binarnog broja, za svaku tvrdnju ako je točna napišite  , ako je netočna
, ako je netočna  . Dakle, npr. ako bi odgovorili bili točno, netočno, točno, netočno, točno, upišite 10101:
. Dakle, npr. ako bi odgovorili bili točno, netočno, točno, netočno, točno, upišite 10101:
 2 > 1
2 > 1
 Umnožak rješenja jednadžbe
Umnožak rješenja jednadžbe 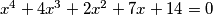 je veći od umnoška rješenja jednadžbe
je veći od umnoška rješenja jednadžbe 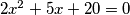
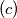
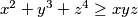 za sve
za sve 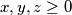
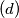 Postoji beskonačni strogo padajući niz pozitivnih realnih brojeva.
Postoji beskonačni strogo padajući niz pozitivnih realnih brojeva.
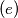 Neka je
Neka je 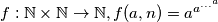 , gdje se
, gdje se  javlja u eksponentu
javlja u eksponentu  puta.
puta. 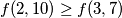 .
.
 , ako je netočna
, ako je netočna  . Dakle, npr. ako bi odgovorili bili točno, netočno, točno, netočno, točno, upišite 10101:
. Dakle, npr. ako bi odgovorili bili točno, netočno, točno, netočno, točno, upišite 10101: 2 > 1
2 > 1 Umnožak rješenja jednadžbe
Umnožak rješenja jednadžbe 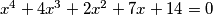 je veći od umnoška rješenja jednadžbe
je veći od umnoška rješenja jednadžbe 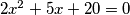
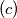
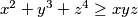 za sve
za sve 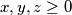
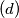 Postoji beskonačni strogo padajući niz pozitivnih realnih brojeva.
Postoji beskonačni strogo padajući niz pozitivnih realnih brojeva.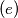 Neka je
Neka je 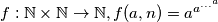 , gdje se
, gdje se  javlja u eksponentu
javlja u eksponentu  puta.
puta. 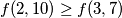 .
. 