Vrijeme: 17:57
Geometrija #3
Neka je  promjer kružnice
promjer kružnice  , i neka je
, i neka je  točka na
točka na  takva da tangenta na
takva da tangenta na  u točki
u točki  siječe pravac
siječe pravac  u točki
u točki  tako da je
tako da je  između
između  i
i  .
.
Neka je  nožište okomice iz
nožište okomice iz  na
na 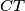 . Ako je
. Ako je 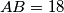 , neka je maksimalna moguća duljina dužine
, neka je maksimalna moguća duljina dužine 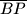 broj
broj 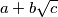 gdje su
gdje su 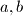 i
i  nenegativni cijeli brojevi, te
nenegativni cijeli brojevi, te  nije djeljiv kvadratom nijednog prirodnog broja osim
nije djeljiv kvadratom nijednog prirodnog broja osim  . (Izraz pod korijenom je skraćen.) Koliko je
. (Izraz pod korijenom je skraćen.) Koliko je 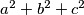 ?
?
