Kako našem akademiku mozak radi nevjerojatnom brzinom, sljedeća tvrdnja sinula mu je u trenutku, ali nije još imao vremena pozabaviti se s njom pa ostavlja na rješavanje vama.
Rad br. 2 - "Jedno rafiniranje poznate nejednakosti." Odredi najveći realan broj 
tako da za sve realne brojeve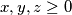 
vrijedi
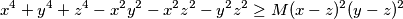
Kako našem akademiku mozak radi nevjerojatnom brzinom, sljedeća tvrdnja sinula mu je u trenutku, ali nije još imao vremena pozabaviti se s njom pa ostavlja na rješavanje vama.
Rad br. 2 - "Jedno rafiniranje poznate nejednakosti." Odredi najveći realan broj $M$ tako da za sve realne brojeve $x,y,z\ge 0$ vrijedi
\[ x^4+y^4+z^4-x^2y^2-x^2z^2-y^2z^2 \ge M(x-z)^2(y-z)^2 \]
