Sljedeća nejednakost mogla bi predstavljati pravu revoluciju u nejednakostima. Možete li i u ovome zadatku pomoći našem akademiku?
Rad br. 3 - "Još jedno rafiniranje AG-a." Odredi najveći realan broj 
takav da za sve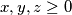 
, takve da je 
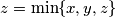vrijedi
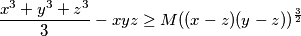
Sljedeća nejednakost mogla bi predstavljati pravu revoluciju u nejednakostima. Možete li i u ovome zadatku pomoći našem akademiku?
Rad br. 3 - "Još jedno rafiniranje AG-a." Odredi najveći realan broj $M$ takav da za sve $x,y,z\ge 0$, takve da je $z=\min\{x,y,z\}$ vrijedi
\[ \frac{x^3+y^3+z^3}{3}-xyz\ge M((x-z)(y-z))^{\frac{3}{2}}\]
