Jednoga dana, naš se je vrli Akademik, koji je svojim istraživanjem produbio poznavanje matematike u raznim područjima - od algebarskih nejednakosti u 3 varijable, preko algebarskih nejednakosti u 4 varijable pa sve do nejednakosti za konveksne funkcije sa 7. derivacijom većom od 4, odlučio pozabaviti jednim od najvažnijih problema u matematici nakon Riemannove hipoteze - rafiniranjem AG nejednakosti i izdati svoj 1941. znanstveni rad. Međutim, genijalac kakav jest, odmah je smislio nekoliko znanstvenih radova, ali kako ima više ideja nego vremena, poslao nam je te probleme na Marinadu jer je čuo da se ovdje skupljaju najbolji mladi matematičari iz Hrvatske. Riješite sljedeće zadatke i pomozite našem akademiku da izda još 5 novih znanstvenih radova!
Rad br. 1 - "Jedno rafiniranje AG-a." Odredi najveći realan  tako da za sve
tako da za sve 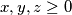 vrijedi
vrijedi
![\frac{x+y+z}{3}-\sqrt[3]{xyz}\ge M(\sqrt{\max\{x,y,z\}}-\sqrt{\min\{x,y,z\}})^2](/media/m/8/0/5/805c762e3e570933de3e86f588938452.png)
Jednoga dana, naš se je vrli Akademik, koji je svojim istraživanjem produbio poznavanje matematike u raznim područjima - od algebarskih nejednakosti u 3 varijable, preko algebarskih nejednakosti u 4 varijable pa sve do nejednakosti za konveksne funkcije sa 7. derivacijom većom od 4, odlučio pozabaviti jednim od najvažnijih problema u matematici nakon Riemannove hipoteze - rafiniranjem AG nejednakosti i izdati svoj 1941. znanstveni rad. Međutim, genijalac kakav jest, odmah je smislio nekoliko znanstvenih radova, ali kako ima više ideja nego vremena, poslao nam je te probleme na Marinadu jer je čuo da se ovdje skupljaju najbolji mladi matematičari iz Hrvatske. Riješite sljedeće zadatke i pomozite našem akademiku da izda još 5 novih znanstvenih radova!
Rad br. 1 - "Jedno rafiniranje AG-a." Odredi najveći realan $M$ tako da za sve $x,y,z\ge 0$ vrijedi
\[ \frac{x+y+z}{3}-\sqrt[3]{xyz}\ge M(\sqrt{\max\{x,y,z\}}-\sqrt{\min\{x,y,z\}})^2 \]
 tako da za sve
tako da za sve 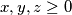 vrijedi
vrijedi![\frac{x+y+z}{3}-\sqrt[3]{xyz}\ge M(\sqrt{\max\{x,y,z\}}-\sqrt{\min\{x,y,z\}})^2](/media/m/8/0/5/805c762e3e570933de3e86f588938452.png)
