Na 
mrežu jediničnih kvadratića postavljeno je 1004 domina dimenzija 
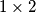(mogu biti vodoravne i okomite) tako da svaka pokriva dva jedinična kvadratića te se nikoje 2 ne dodiruju, čak ni u vrhovima.
Odredi MINimalan 
za koji je to moguće.
Na $n \times n$ mrežu jediničnih kvadratića postavljeno je 1004 domina dimenzija $ 1\times 2$ (mogu biti vodoravne i okomite) tako da svaka pokriva dva jedinična kvadratića te se nikoje 2 ne dodiruju, čak ni u vrhovima.
Odredi MINimalan $n$ za koji je to moguće.
