Za koje sve prirodne brojeve

postoje prirodni brojevi
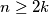
,

i
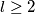
takvi da je
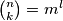
?
For which positive integers

do there exist positive integers
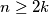
,

and
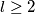
such that
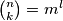
?
[lang=hr]
Za koje sve prirodne brojeve $k$ postoje prirodni brojevi $n \geq 2k$, $m$ i $l \geq 2$ takvi da je $\binom{n}{k} = m^l$ ?
[/lang]
[lang=en]
For which positive integers $k$ do there exist positive integers $n \geq 2k$, $m$ and $l \geq 2$ such that $\binom{n}{k} = m^l$ ?
[/lang]