Vrijeme: 18:07
Kineska matura | Chinese Final Exam #5
Trokut  upisan je u kružnicu
upisan je u kružnicu  pri čemu
pri čemu 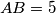 ,
, 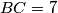 i
i 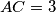 . Simetrala unutarnjeg kuta
. Simetrala unutarnjeg kuta  siječe
siječe  u
u  i kružnicu drugi put
i kružnicu drugi put  u točki
u točki  . Neka je
. Neka je  kružnica promjera
kružnica promjera  . Kružnice
. Kružnice  i
i  sijeku se u
sijeku se u  i
i  . Imamo
. Imamo 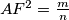 , gdje m i n su relativno prosti prirodni brojevi. Nađi
, gdje m i n su relativno prosti prirodni brojevi. Nađi 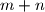 .
.
 upisan je u kružnicu
upisan je u kružnicu  pri čemu
pri čemu 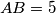 ,
, 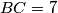 i
i 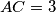 . Simetrala unutarnjeg kuta
. Simetrala unutarnjeg kuta  siječe
siječe  u
u  i kružnicu drugi put
i kružnicu drugi put  u točki
u točki  . Neka je
. Neka je  kružnica promjera
kružnica promjera  . Kružnice
. Kružnice  i
i  sijeku se u
sijeku se u  i
i  . Imamo
. Imamo 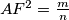 , gdje m i n su relativno prosti prirodni brojevi. Nađi
, gdje m i n su relativno prosti prirodni brojevi. Nađi 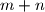 .
. In the triangle  , which is inscribed in the circle
, which is inscribed in the circle  , it is known that
, it is known that 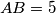 ,
, 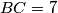 and
and 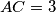 . The two points
. The two points  and
and  are the points where the bisector of angle
are the points where the bisector of angle  intersects side
intersects side  and circle
and circle  , respectively. Let
, respectively. Let  be the circle with a diameter
be the circle with a diameter  . The circles
. The circles  and
and  intersect at points
intersect at points  and
and  . Additionally,
. Additionally, 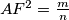 , where
, where  and
and  are relatively prime natural numbers. What is the value of
are relatively prime natural numbers. What is the value of  ?
?
 , which is inscribed in the circle
, which is inscribed in the circle  , it is known that
, it is known that 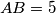 ,
, 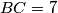 and
and 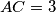 . The two points
. The two points  and
and  are the points where the bisector of angle
are the points where the bisector of angle  intersects side
intersects side  and circle
and circle  , respectively. Let
, respectively. Let  be the circle with a diameter
be the circle with a diameter  . The circles
. The circles  and
and  intersect at points
intersect at points  and
and  . Additionally,
. Additionally, 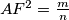 , where
, where  and
and  are relatively prime natural numbers. What is the value of
are relatively prime natural numbers. What is the value of  ?
? 