Vrijeme: 18:09
Kineska matura | Chinese Final Exam #3
Dan je pravilan šesterokut sa središtem u ishodištu kompleksne ravnine čije su nasuprotne stranice udaljene za jednu jedinicu. Jedan par stranica je paralelan sa imaginarnom osi. Označimo sa  dio ravnine izvan šesterokuta. Nadalje neka je
dio ravnine izvan šesterokuta. Nadalje neka je 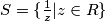 . Tada se površina
. Tada se površina  može iskazati kao
može iskazati kao 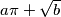 , gdje
, gdje  i
i  su prirodni brojevi. Nađi
su prirodni brojevi. Nađi  .
.
 dio ravnine izvan šesterokuta. Nadalje neka je
dio ravnine izvan šesterokuta. Nadalje neka je 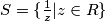 . Tada se površina
. Tada se površina  može iskazati kao
može iskazati kao 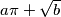 , gdje
, gdje  i
i  su prirodni brojevi. Nađi
su prirodni brojevi. Nađi  .
. The opposite pairs of sides of a regular hexagon in the complex plane with the center at the origin are one unit apart. One pair of sides lies parallel to the imaginary axis. If  is the part of the plane outside the hexagon, and
is the part of the plane outside the hexagon, and 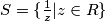 , the area
, the area  can be expressed as
can be expressed as 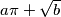 , where
, where  and
and  are natural numbers. What is the value of
are natural numbers. What is the value of  ?
?
 is the part of the plane outside the hexagon, and
is the part of the plane outside the hexagon, and 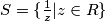 , the area
, the area  can be expressed as
can be expressed as 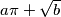 , where
, where  and
and  are natural numbers. What is the value of
are natural numbers. What is the value of  ?
? 