Vrijeme: 18:09
Kineska matura | Chinese Final Exam #2
Kružnice  i
i  sijeku se u
sijeku se u  i
i  i neka je dužina
i neka je dužina  promjer
promjer  . Tangenta u
. Tangenta u  kružnice
kružnice  siječe
siječe  u
u  .
.  siječe
siječe  u
u  , a neka
, a neka 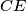 siječe
siječe  u
u  . Neka je
. Neka je  točka na dužini
točka na dužini 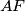 . Neka
. Neka 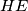 siječe
siječe  u
u  i neka se
i neka se 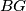 i
i  sijeku u
sijeku u  . Nadalje, igrom slučaja ispalo je
. Nadalje, igrom slučaja ispalo je 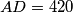 ,
, 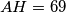 ,
, 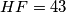 . Odredi duljinu dužine
. Odredi duljinu dužine  . Zaokružite rezultat na 6 decimala.
. Zaokružite rezultat na 6 decimala.
 i
i  sijeku se u
sijeku se u  i
i  i neka je dužina
i neka je dužina  promjer
promjer  . Tangenta u
. Tangenta u  kružnice
kružnice  siječe
siječe  u
u  .
.  siječe
siječe  u
u  , a neka
, a neka 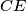 siječe
siječe  u
u  . Neka je
. Neka je  točka na dužini
točka na dužini 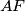 . Neka
. Neka 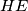 siječe
siječe  u
u  i neka se
i neka se 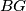 i
i  sijeku u
sijeku u  . Nadalje, igrom slučaja ispalo je
. Nadalje, igrom slučaja ispalo je 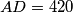 ,
, 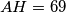 ,
, 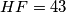 . Odredi duljinu dužine
. Odredi duljinu dužine  . Zaokružite rezultat na 6 decimala.
. Zaokružite rezultat na 6 decimala. The circles  and
and  intersect at
intersect at  and
and  . Let the segment
. Let the segment  be the diameter of
be the diameter of  . The tangent of
. The tangent of  through point
through point  meets
meets  at
at  .
.  meets
meets  at
at  and
and 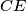 meets
meets  at
at  . Let
. Let  be a point of the segment
be a point of the segment 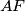 .
. 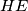 and
and  intersect at
intersect at  , and
, and 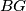 and
and  intersect at
intersect at  . Coincidentally, it turns out
. Coincidentally, it turns out 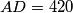 ,
, 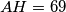 ,
, 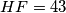 . Determine the length of the segment
. Determine the length of the segment  . Round the result to 6 decimal places.
. Round the result to 6 decimal places.
 and
and  intersect at
intersect at  and
and  . Let the segment
. Let the segment  be the diameter of
be the diameter of  . The tangent of
. The tangent of  through point
through point  meets
meets  at
at  .
.  meets
meets  at
at  and
and 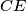 meets
meets  at
at  . Let
. Let  be a point of the segment
be a point of the segment 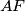 .
. 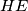 and
and  intersect at
intersect at  , and
, and 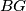 and
and  intersect at
intersect at  . Coincidentally, it turns out
. Coincidentally, it turns out 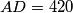 ,
, 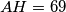 ,
, 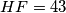 . Determine the length of the segment
. Determine the length of the segment  . Round the result to 6 decimal places.
. Round the result to 6 decimal places. 