Vrijeme: 18:09
Kineska matura | Chinese Final Exam #4
Upisana kružnica  od
od  dira
dira  u
u  . Neka je
. Neka je 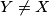 drugo sjecište
drugo sjecište 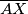 sa
sa  . Točke
. Točke  i
i  leže na
leže na  i
i  , redom, tako da
, redom, tako da 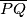 je tangenta na
je tangenta na  u
u  . Pretpostavi da
. Pretpostavi da 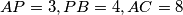 i
i 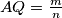 , gdje
, gdje  i
i  su relativno prosti prirodni brojevi. Nađi
su relativno prosti prirodni brojevi. Nađi  .
.
 od
od  dira
dira  u
u  . Neka je
. Neka je 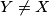 drugo sjecište
drugo sjecište 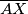 sa
sa  . Točke
. Točke  i
i  leže na
leže na  i
i  , redom, tako da
, redom, tako da 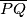 je tangenta na
je tangenta na  u
u  . Pretpostavi da
. Pretpostavi da 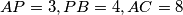 i
i 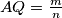 , gdje
, gdje  i
i  su relativno prosti prirodni brojevi. Nađi
su relativno prosti prirodni brojevi. Nađi  .
. The inscribed circle  of the triangle
of the triangle  is tangent to
is tangent to  at
at  . Let
. Let 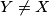 be the other intersection of
be the other intersection of 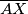 and
and  . The points
. The points  and
and  lie on
lie on  and
and  , respectively, so that
, respectively, so that 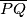 is tangent to
is tangent to  at
at  . It is known that
. It is known that 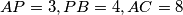 and
and 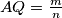 , where
, where  and
and  are relatively prime natural numbers. What is the value of
are relatively prime natural numbers. What is the value of  ?
?
 of the triangle
of the triangle  is tangent to
is tangent to  at
at  . Let
. Let 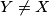 be the other intersection of
be the other intersection of 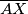 and
and  . The points
. The points  and
and  lie on
lie on  and
and  , respectively, so that
, respectively, so that 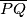 is tangent to
is tangent to  at
at  . It is known that
. It is known that 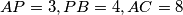 and
and 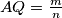 , where
, where  and
and  are relatively prime natural numbers. What is the value of
are relatively prime natural numbers. What is the value of  ?
? 