Vrijeme: 18:09
Henτ | Henτ #1
Kružnica 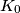 ima polumjer
ima polumjer  i
i  je točka na toj kružnici. Kružnica
je točka na toj kružnici. Kružnica 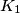 ima polumjer
ima polumjer 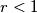 i s unutrašnje strane dira
i s unutrašnje strane dira 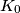 u točki
u točki  . Točka
. Točka  leži na kružnici
leži na kružnici 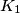
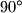 u smjeru obrnutom od smjera kazaljke na satu s obzirom na
u smjeru obrnutom od smjera kazaljke na satu s obzirom na  . Kružnica
. Kružnica 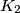 ima polumjer
ima polumjer 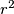 i s unutrašnje strane dira
i s unutrašnje strane dira 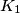 u točki
u točki  . Na navedeni način konstruiran je niz kružnica
. Na navedeni način konstruiran je niz kružnica 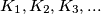 i točaka
i točaka 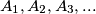 na navedenim kružnicama, pri čemu kružnica
na navedenim kružnicama, pri čemu kružnica 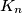 ima radijus
ima radijus 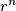 i iznutra dodiruje kružnicu
i iznutra dodiruje kružnicu 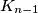 u točki
u točki 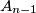 . Također, točka
. Također, točka 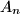 nalazi se na
nalazi se na 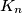
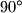 obrnuto od smjera kazaljke na satu od točke
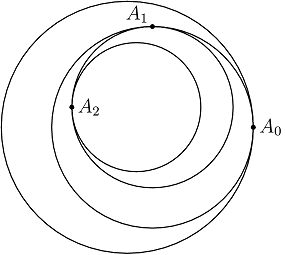
obrnuto od smjera kazaljke na satu od točke 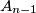 , kao što je prikazano na slici.
, kao što je prikazano na slici.
Postoji točka koja se nalazi unutar svih kružnica. Kada
koja se nalazi unutar svih kružnica. Kada  iznosi
iznosi 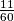 , udaljenost središta
, udaljenost središta 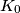 od
od  je
je 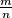 , gdje su
, gdje su  i
i  relativno prosti prirodni brojevi. Koliko iznosi
relativno prosti prirodni brojevi. Koliko iznosi  ?
?
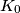 ima polumjer
ima polumjer  i
i  je točka na toj kružnici. Kružnica
je točka na toj kružnici. Kružnica 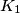 ima polumjer
ima polumjer 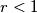 i s unutrašnje strane dira
i s unutrašnje strane dira 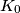 u točki
u točki  . Točka
. Točka  leži na kružnici
leži na kružnici 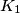
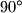 u smjeru obrnutom od smjera kazaljke na satu s obzirom na
u smjeru obrnutom od smjera kazaljke na satu s obzirom na  . Kružnica
. Kružnica 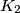 ima polumjer
ima polumjer 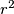 i s unutrašnje strane dira
i s unutrašnje strane dira 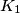 u točki
u točki  . Na navedeni način konstruiran je niz kružnica
. Na navedeni način konstruiran je niz kružnica 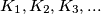 i točaka
i točaka 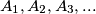 na navedenim kružnicama, pri čemu kružnica
na navedenim kružnicama, pri čemu kružnica 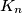 ima radijus
ima radijus 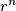 i iznutra dodiruje kružnicu
i iznutra dodiruje kružnicu 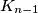 u točki
u točki 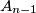 . Također, točka
. Također, točka 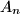 nalazi se na
nalazi se na 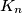
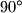 obrnuto od smjera kazaljke na satu od točke
obrnuto od smjera kazaljke na satu od točke 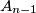 , kao što je prikazano na slici.
, kao što je prikazano na slici. Postoji točka
 koja se nalazi unutar svih kružnica. Kada
koja se nalazi unutar svih kružnica. Kada  iznosi
iznosi 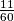 , udaljenost središta
, udaljenost središta 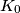 od
od  je
je 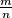 , gdje su
, gdje su  i
i  relativno prosti prirodni brojevi. Koliko iznosi
relativno prosti prirodni brojevi. Koliko iznosi  ?
?
Radius of a circle 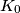 is
is  .
.  is a point on that circle. Radius of a circle
is a point on that circle. Radius of a circle 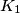 is
is  .
. 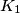 touches
touches 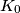 internally at
internally at  . We choose a point
. We choose a point  so that it lies
so that it lies 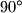 counterclockwise from
counterclockwise from  on
on 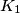 . Circle
. Circle 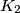 has a radius
has a radius 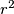 and touches
and touches 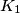 internally at point
internally at point  . This way we have constructed a sequence of circles
. This way we have constructed a sequence of circles 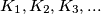 and a sequence of points
and a sequence of points 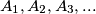 on said circles, where circle
on said circles, where circle 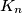 has a radius
has a radius 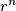 and touches the circle
and touches the circle 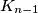 internally at
internally at 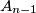 . Also,
. Also, 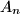 lies
lies 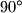 counterclockwise from
counterclockwise from 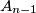 on the circle
on the circle 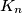 , as shown in the figure below.
, as shown in the figure below.
There exists a point inside all these circles. When
inside all these circles. When 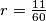 , the distance between the center of
, the distance between the center of 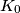 and
and  is
is 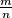 , where
, where  and
and  are relatively prime. Find
are relatively prime. Find  .
.
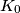 is
is  .
.  is a point on that circle. Radius of a circle
is a point on that circle. Radius of a circle 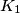 is
is 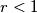 .
. 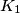 touches
touches 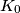 internally at
internally at  . We choose a point
. We choose a point  so that it lies
so that it lies 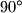 counterclockwise from
counterclockwise from  on
on 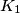 . Circle
. Circle 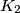 has a radius
has a radius 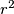 and touches
and touches 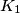 internally at point
internally at point  . This way we have constructed a sequence of circles
. This way we have constructed a sequence of circles 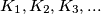 and a sequence of points
and a sequence of points 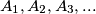 on said circles, where circle
on said circles, where circle 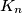 has a radius
has a radius 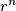 and touches the circle
and touches the circle 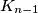 internally at
internally at 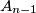 . Also,
. Also, 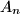 lies
lies 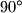 counterclockwise from
counterclockwise from 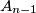 on the circle
on the circle 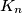 , as shown in the figure below.
, as shown in the figure below. There exists a point
 inside all these circles. When
inside all these circles. When 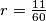 , the distance between the center of
, the distance between the center of 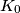 and
and  is
is 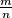 , where
, where  and
and  are relatively prime. Find
are relatively prime. Find  .
.
