Vrijeme: 18:03
Henτ | Henτ #2
Dan je trokut  sa
sa 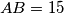 ,
, 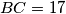 i
i 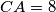 . Kružnica
. Kružnica 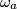 sa središtem na
sa središtem na  dira dužine
dira dužine  i
i  . Kružnice
. Kružnice 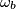 i
i 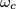 su definirane analogno. Četvrtu kružnicu
su definirane analogno. Četvrtu kružnicu  radijusa
radijusa  iznutra diraju
iznutra diraju 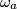 ,
, 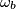 i
i 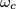 .
.  se može zapisati kao
se može zapisati kao 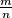 , gdje su
, gdje su  i
i  relativno prosti prirodni brojevi. Izračunaj
relativno prosti prirodni brojevi. Izračunaj  .
.
 sa
sa 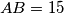 ,
, 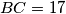 i
i 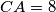 . Kružnica
. Kružnica 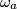 sa središtem na
sa središtem na  dira dužine
dira dužine  i
i  . Kružnice
. Kružnice 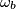 i
i 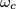 su definirane analogno. Četvrtu kružnicu
su definirane analogno. Četvrtu kružnicu  radijusa
radijusa  iznutra diraju
iznutra diraju 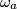 ,
, 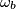 i
i 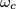 .
.  se može zapisati kao
se može zapisati kao 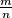 , gdje su
, gdje su  i
i  relativno prosti prirodni brojevi. Izračunaj
relativno prosti prirodni brojevi. Izračunaj  .
.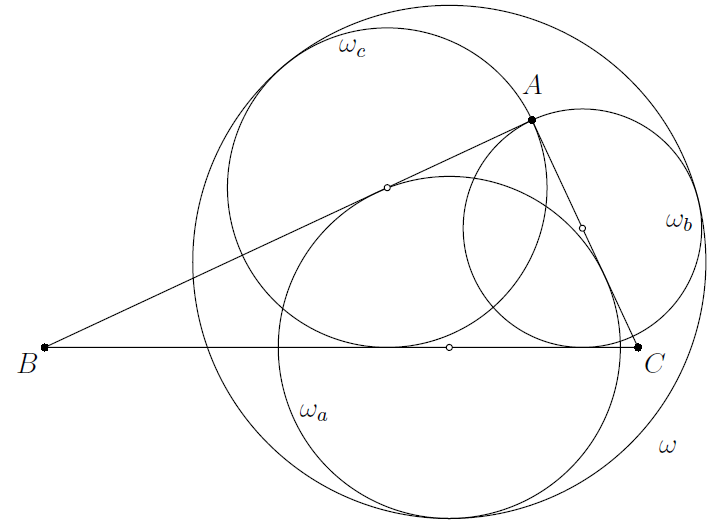
In triangle  , the side lengths are
, the side lengths are 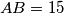 ,
, 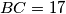 and
and 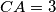 . The segments
. The segments  and
and  touch the circle
touch the circle 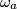 whose center lies on the segment
whose center lies on the segment  . Circles
. Circles 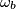 and
and 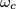 are defined analogously. The fourth circle
are defined analogously. The fourth circle  has a radius
has a radius  and is touched internally by
and is touched internally by 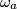 ,
, 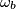 and
and 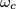 .
.  can be written as
can be written as 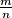 , where
, where  and
and  are relatively prime natural numbers. Calculate
are relatively prime natural numbers. Calculate 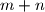
 , the side lengths are
, the side lengths are 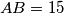 ,
, 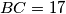 and
and 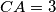 . The segments
. The segments  and
and  touch the circle
touch the circle 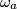 whose center lies on the segment
whose center lies on the segment  . Circles
. Circles 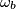 and
and 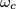 are defined analogously. The fourth circle
are defined analogously. The fourth circle  has a radius
has a radius  and is touched internally by
and is touched internally by 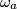 ,
, 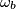 and
and 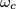 .
.  can be written as
can be written as 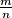 , where
, where  and
and  are relatively prime natural numbers. Calculate
are relatively prime natural numbers. Calculate