Vrijeme: 18:03
Henτ | Henτ #4
Kružnica  radijusa
radijusa  izvana se dira sa kružnicama
izvana se dira sa kružnicama  i
i  , pri čemu su pravci
, pri čemu su pravci 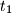 i
i 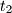 vanjske tangente na sve tri kružnice. Četvrtu kružnicu
vanjske tangente na sve tri kružnice. Četvrtu kružnicu  kružnice
kružnice  i
i  diraju iznutra. Neka su
diraju iznutra. Neka su  i
i  radijusa
radijusa 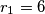 i
i 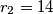 najveće kružnice koje se mogu upisati odsječcima koje određuju
najveće kružnice koje se mogu upisati odsječcima koje određuju  , pravci
, pravci 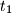 i
i 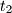 te ne sadržavaju
te ne sadržavaju  . Radijus kružnice
. Radijus kružnice  može se zapisati kao
može se zapisati kao 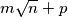 gdje su
gdje su  ,
,  i
i  prirodni brojevi, a
prirodni brojevi, a  je kvadratno slobodan. Izračunaj
je kvadratno slobodan. Izračunaj  .
.
 radijusa
radijusa  izvana se dira sa kružnicama
izvana se dira sa kružnicama  i
i  , pri čemu su pravci
, pri čemu su pravci 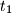 i
i 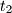 vanjske tangente na sve tri kružnice. Četvrtu kružnicu
vanjske tangente na sve tri kružnice. Četvrtu kružnicu  kružnice
kružnice  i
i  diraju iznutra. Neka su
diraju iznutra. Neka su  i
i  radijusa
radijusa 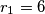 i
i 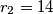 najveće kružnice koje se mogu upisati odsječcima koje određuju
najveće kružnice koje se mogu upisati odsječcima koje određuju  , pravci
, pravci 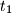 i
i 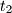 te ne sadržavaju
te ne sadržavaju  . Radijus kružnice
. Radijus kružnice  može se zapisati kao
može se zapisati kao 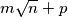 gdje su
gdje su  ,
,  i
i  prirodni brojevi, a
prirodni brojevi, a  je kvadratno slobodan. Izračunaj
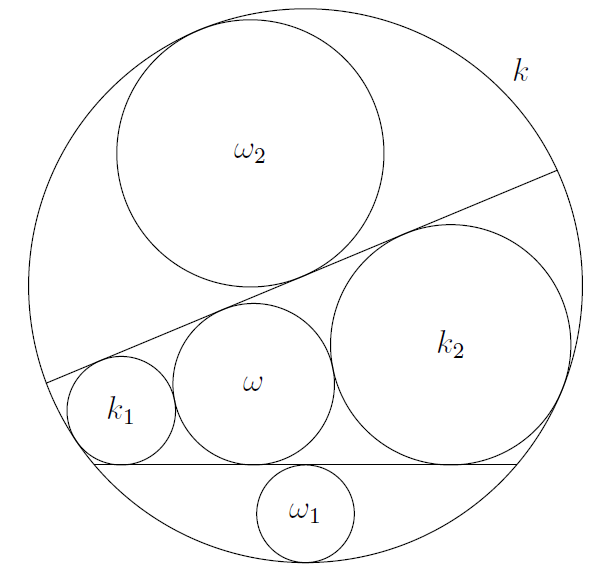
je kvadratno slobodan. Izračunaj  .
.
The circle  of radius
of radius  touches the circles
touches the circles  and
and  externally, and lines
externally, and lines 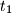 and
and 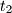 are the external tangents to all three circles. The circles
are the external tangents to all three circles. The circles  and
and  are tangent externally to the fourth circle
are tangent externally to the fourth circle  . Let
. Let  and
and  of radii
of radii 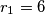 and
and 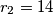 be the largest circles that can be inscribed in the areas determined by
be the largest circles that can be inscribed in the areas determined by  ,
, 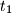 and
and 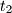 , excluding the area that contains
, excluding the area that contains  . The radius of
. The radius of  can be written as
can be written as 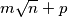 where
where  ,
,  and
and  are natural numbers, and
are natural numbers, and  is not divisible by any perfect square (except
is not divisible by any perfect square (except  ). Calculate
). Calculate  .
.
 of radius
of radius  touches the circles
touches the circles  and
and  externally, and lines
externally, and lines 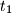 and
and 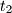 are the external tangents to all three circles. The circles
are the external tangents to all three circles. The circles  and
and  are tangent externally to the fourth circle
are tangent externally to the fourth circle  . Let
. Let  and
and  of radii
of radii 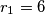 and
and 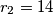 be the largest circles that can be inscribed in the areas determined by
be the largest circles that can be inscribed in the areas determined by  ,
, 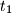 and
and 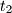 , excluding the area that contains
, excluding the area that contains  . The radius of
. The radius of  can be written as
can be written as 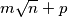 where
where  ,
,  and
and  are natural numbers, and
are natural numbers, and  is not divisible by any perfect square (except
is not divisible by any perfect square (except  ). Calculate
). Calculate  .
.
