Vrijeme: 18:03
Henτ | Henτ #3
Neka je  najveća kružnica koja se može upisati u manji odsječak koji određuju pravac
najveća kružnica koja se može upisati u manji odsječak koji određuju pravac  i kružnica
i kružnica  radijusa
radijusa 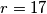 . Kružnica
. Kružnica  sukladna
sukladna  dira
dira  i sadržana je u većem odsječku koji
i sadržana je u većem odsječku koji  odsjeca od
odsjeca od  . Još dvije kružnice
. Još dvije kružnice  i
i 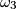 radijusa
radijusa 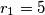 i
i 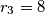 diraju
diraju  ,
,  izvana i
izvana i  iznutra. Izračunaj radijus
iznutra. Izračunaj radijus  .
.
 najveća kružnica koja se može upisati u manji odsječak koji određuju pravac
najveća kružnica koja se može upisati u manji odsječak koji određuju pravac  i kružnica
i kružnica  radijusa
radijusa 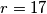 . Kružnica
. Kružnica  sukladna
sukladna  dira
dira  i sadržana je u većem odsječku koji
i sadržana je u većem odsječku koji  odsjeca od
odsjeca od  . Još dvije kružnice
. Još dvije kružnice  i
i 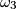 radijusa
radijusa 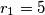 i
i 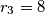 diraju
diraju  ,
,  izvana i
izvana i  iznutra. Izračunaj radijus
iznutra. Izračunaj radijus  .
.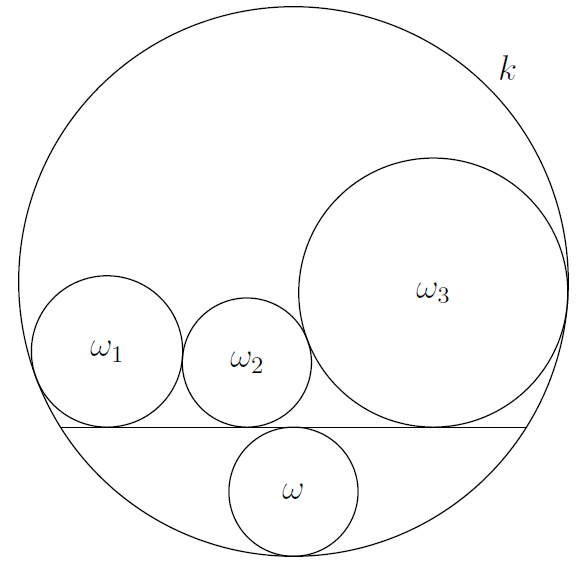
Let  be the largest circle that can be inscribed in the smaller region determined by line
be the largest circle that can be inscribed in the smaller region determined by line  and circle
and circle  of radius
of radius 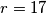 . The circle
. The circle  is congruent to
is congruent to  , touches
, touches  , and is contained inside the larger region determined by
, and is contained inside the larger region determined by  and
and  . Two more circles,
. Two more circles,  and
and 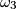 of radii
of radii 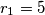 and
and 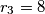 , touch
, touch  and
and  externally and
externally and  internally. Calculate the radius of
internally. Calculate the radius of  .
.
 be the largest circle that can be inscribed in the smaller region determined by line
be the largest circle that can be inscribed in the smaller region determined by line  and circle
and circle  of radius
of radius 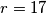 . The circle
. The circle  is congruent to
is congruent to  , touches
, touches  , and is contained inside the larger region determined by
, and is contained inside the larger region determined by  and
and  . Two more circles,
. Two more circles,  and
and 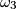 of radii
of radii 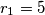 and
and 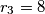 , touch
, touch  and
and  externally and
externally and  internally. Calculate the radius of
internally. Calculate the radius of  .
.
