Vrijeme: 18:06
Legija loptica | Legion of balls #1
Dane su tri kutije loptica 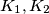 i
i 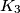 takve da svaka sadrži točno jednu lopticu. Dozvoljene su sljedeće operacije:
takve da svaka sadrži točno jednu lopticu. Dozvoljene su sljedeće operacije: 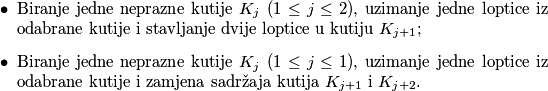 Odredi najveći broj loptica koji je moguće postići u kutiji
Odredi najveći broj loptica koji je moguće postići u kutiji 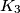 gornjim operacijama.
gornjim operacijama.
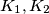 i
i 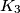 takve da svaka sadrži točno jednu lopticu. Dozvoljene su sljedeće operacije:
takve da svaka sadrži točno jednu lopticu. Dozvoljene su sljedeće operacije: 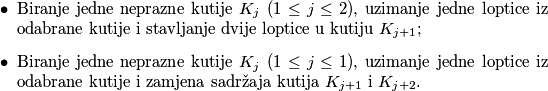 Odredi najveći broj loptica koji je moguće postići u kutiji
Odredi najveći broj loptica koji je moguće postići u kutiji 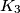 gornjim operacijama.
gornjim operacijama. We're given three boxes 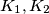 and
and 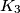 such that each of them contains exactly one ball. The following operations are allowed:
such that each of them contains exactly one ball. The following operations are allowed: 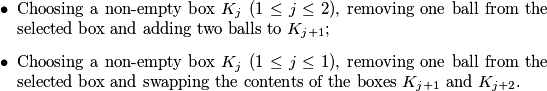 Determine the largest obtainable number of balls in
Determine the largest obtainable number of balls in 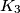 using the operations above.
using the operations above.
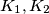 and
and 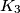 such that each of them contains exactly one ball. The following operations are allowed:
such that each of them contains exactly one ball. The following operations are allowed: 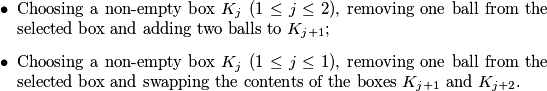 Determine the largest obtainable number of balls in
Determine the largest obtainable number of balls in 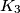 using the operations above.
using the operations above. 