Vrijeme: 18:07
Legija loptica | Legion of balls #4
Dano je pet kutija loptica 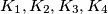 i
i 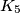 tako da svaka sadrži točno jednu lopticu. Dozvoljene su sljedeće operacije:
tako da svaka sadrži točno jednu lopticu. Dozvoljene su sljedeće operacije: 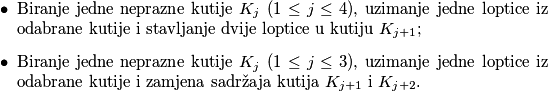 Najveći broj loptica koji je moguće postići u kutiji
Najveći broj loptica koji je moguće postići u kutiji 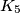 gornjim operacijama možemo zapisati u obliku
gornjim operacijama možemo zapisati u obliku 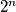 . Odredi
. Odredi 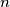 .
.
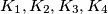 i
i 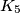 tako da svaka sadrži točno jednu lopticu. Dozvoljene su sljedeće operacije:
tako da svaka sadrži točno jednu lopticu. Dozvoljene su sljedeće operacije: 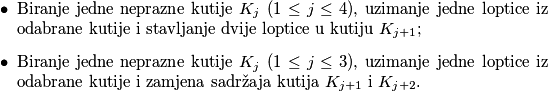 Najveći broj loptica koji je moguće postići u kutiji
Najveći broj loptica koji je moguće postići u kutiji 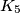 gornjim operacijama možemo zapisati u obliku
gornjim operacijama možemo zapisati u obliku 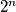 . Odredi
. Odredi 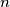 .
. We're given five boxes 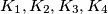 and
and 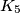 such that each of them contains exactly one ball. The following operations are allowed:
such that each of them contains exactly one ball. The following operations are allowed: 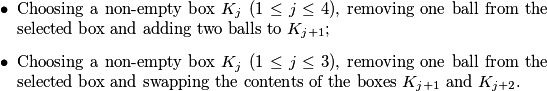 The largest obtainable number of balls in
The largest obtainable number of balls in 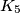 using the operations above can be written as
using the operations above can be written as 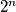 . Determine
. Determine 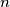 .
.
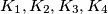 and
and 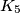 such that each of them contains exactly one ball. The following operations are allowed:
such that each of them contains exactly one ball. The following operations are allowed: 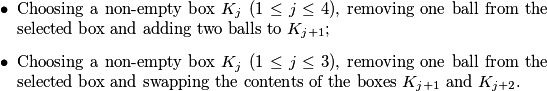 The largest obtainable number of balls in
The largest obtainable number of balls in 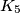 using the operations above can be written as
using the operations above can be written as 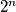 . Determine
. Determine 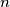 .
. 