Vrijeme: 18:05
Iz dobrih starih spisa | Good Old Times #4
U trapezu  s osnovicama
s osnovicama  i
i  je
je 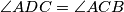 . Odredi duljinu dužine
. Odredi duljinu dužine  ako je duljina srednjice trapeza
ako je duljina srednjice trapeza  , a duljine osnovica odnose se kao
, a duljine osnovica odnose se kao 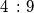 .
.
 s osnovicama
s osnovicama  i
i  je
je 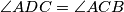 . Odredi duljinu dužine
. Odredi duljinu dužine  ako je duljina srednjice trapeza
ako je duljina srednjice trapeza  , a duljine osnovica odnose se kao
, a duljine osnovica odnose se kao 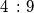 .
. In the trapezium  , the bases are
, the bases are  and
and  . It is known that
. It is known that 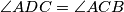 , that the length of the midline is
, that the length of the midline is  , and that the ratio of the lengths of the bases is
, and that the ratio of the lengths of the bases is 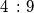 . What is the length of the segment
. What is the length of the segment  ?
?
 , the bases are
, the bases are  and
and  . It is known that
. It is known that 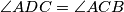 , that the length of the midline is
, that the length of the midline is  , and that the ratio of the lengths of the bases is
, and that the ratio of the lengths of the bases is 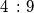 . What is the length of the segment
. What is the length of the segment  ?
? 