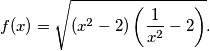Vrijeme: 18:04
Pec na domenu | Domain no-no #1
Prirodna domena funkcije je najveći podskup realnih brojeva na kojem je funkcija dobro definirana. U ovom lancu zadataka svaki se skup može prikazati kao konačna unija disjunktnih intervala, a njegovu duljinu ćemo definirati kao zbroj duljina spomenutih intervala (duljinu intervala definiramo kao razliku njegove gornje i donje granice). Primjerice duljina skupa ![\{17,18\} = [17,17]\cup [18,18]](/media/m/f/e/9/fe949b8b64ec62b8bbcc831e1e45cba6.png) je
je 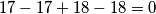 , dok je duljina skupa
, dok je duljina skupa 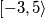 jednaka
jednaka 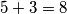 . Duljina praznog skupa je
. Duljina praznog skupa je 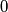 i neće se pojavljivati duljine neograničenih skupova. Odredi duljinu prirodne domene funkcije
i neće se pojavljivati duljine neograničenih skupova. Odredi duljinu prirodne domene funkcije 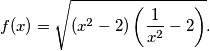
![\{17,18\} = [17,17]\cup [18,18]](/media/m/f/e/9/fe949b8b64ec62b8bbcc831e1e45cba6.png) je
je 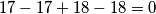 , dok je duljina skupa
, dok je duljina skupa 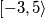 jednaka
jednaka 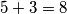 . Duljina praznog skupa je
. Duljina praznog skupa je 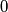 i neće se pojavljivati duljine neograničenih skupova. Odredi duljinu prirodne domene funkcije
i neće se pojavljivati duljine neograničenih skupova. Odredi duljinu prirodne domene funkcije 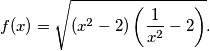
Natural domain of a function is the largest subset of real numbers on which the function is well defined. In this chain of problems every set can be represented as a finite union of disjoint intervals, and we define its length as a sum of the lengths of the mentioned intervals (length of an interval is a difference between its upper and lower bounds). For example the length of the set ![\{17,18\} = [17,17]\cup [18,18]](/media/m/f/e/9/fe949b8b64ec62b8bbcc831e1e45cba6.png) is
is 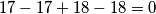 , while the length of the set
, while the length of the set 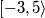 equals
equals 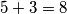 . Length of an empty set is
. Length of an empty set is 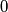 and there won't be unbounded sets. Determine the length of the natural domain of the function
and there won't be unbounded sets. Determine the length of the natural domain of the function 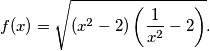
![\{17,18\} = [17,17]\cup [18,18]](/media/m/f/e/9/fe949b8b64ec62b8bbcc831e1e45cba6.png) is
is 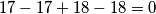 , while the length of the set
, while the length of the set 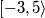 equals
equals 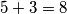 . Length of an empty set is
. Length of an empty set is 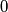 and there won't be unbounded sets. Determine the length of the natural domain of the function
and there won't be unbounded sets. Determine the length of the natural domain of the function