Neka
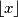
označava najveći cijeli broj koji nije veći od

. Odredi duljinu prirodne domene funkcije
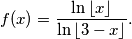
Let
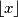
represent the largest integer that is not greater than

. Determine the length of the natural domain of the function
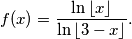
[lang=hr]
Neka \(\left \lfloor x \right \rfloor \) označava najveći cijeli broj koji nije veći od \(x\). Odredi duljinu prirodne domene funkcije
\[f(x)=\dfrac{\ln \left \lfloor x \right \rfloor }{\ln \left \lfloor 3-x \right \rfloor }.\]
[/lang]
[lang=en]
Let \(\left \lfloor x \right \rfloor \) represent the largest integer that is not greater than \(x\). Determine the length of the natural domain of the function
\[f(x)=\dfrac{\ln \left \lfloor x \right \rfloor }{\ln \left \lfloor 3-x \right \rfloor }.\]
[/lang]