Vrijeme: 18:07
Pec na domenu | Domain no-no #4
Neka je 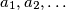 beskonačni niz realnih brojeva zadan s
beskonačni niz realnih brojeva zadan s 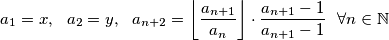 Odredi najmanji prirodan broj
Odredi najmanji prirodan broj  takav da za sve
takav da za sve 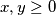 postoji broj
postoji broj 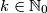 ,
, 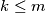 takav da
takav da 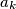 nije dobro definiran.
nije dobro definiran.
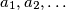 beskonačni niz realnih brojeva zadan s
beskonačni niz realnih brojeva zadan s 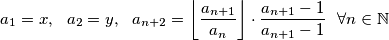 Odredi najmanji prirodan broj
Odredi najmanji prirodan broj  takav da za sve
takav da za sve 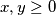 postoji broj
postoji broj 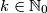 ,
, 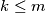 takav da
takav da 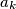 nije dobro definiran.
nije dobro definiran. Let 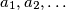 be an infinite sequence of real numbers given by
be an infinite sequence of real numbers given by 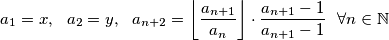 Determine the least positive integer
Determine the least positive integer  such that for all
such that for all 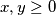 there exists a nonnegative integer
there exists a nonnegative integer 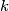 ,
, 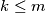 such that
such that 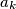 is not well defined.
is not well defined.
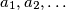 be an infinite sequence of real numbers given by
be an infinite sequence of real numbers given by 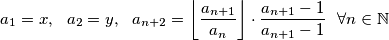 Determine the least positive integer
Determine the least positive integer  such that for all
such that for all 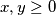 there exists a nonnegative integer
there exists a nonnegative integer 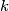 ,
, 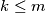 such that
such that 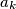 is not well defined.
is not well defined. 