Vrijeme: 18:06
Podijeljeni zajedno | Divided Together #1
U ovom lancu, za dva prirodna broja  i
i  , s
, s 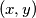 označavat ćemo najveći zajednički djelitelj od
označavat ćemo najveći zajednički djelitelj od  i
i  . Neka su
. Neka su  prirodni brojevi takvi da je
prirodni brojevi takvi da je 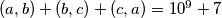 . Odredi najmanju vrijednost koju može poprimiti
. Odredi najmanju vrijednost koju može poprimiti 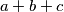 . Broj
. Broj 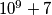 je prost.
je prost.
 i
i  , s
, s 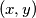 označavat ćemo najveći zajednički djelitelj od
označavat ćemo najveći zajednički djelitelj od  i
i  . Neka su
. Neka su  prirodni brojevi takvi da je
prirodni brojevi takvi da je 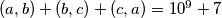 . Odredi najmanju vrijednost koju može poprimiti
. Odredi najmanju vrijednost koju može poprimiti 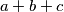 . Broj
. Broj 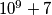 je prost.
je prost. In this chain, for positive integers  and
and  , we'll denote the greatest common divisor of
, we'll denote the greatest common divisor of  and
and  with
with 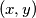 . Let
. Let  be positive integers such that
be positive integers such that 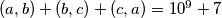 . Find the least possible value that
. Find the least possible value that 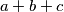 can obtain. The number
can obtain. The number 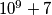 is prime.
is prime.
 and
and  , we'll denote the greatest common divisor of
, we'll denote the greatest common divisor of  and
and  with
with 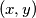 . Let
. Let  be positive integers such that
be positive integers such that 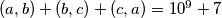 . Find the least possible value that
. Find the least possible value that 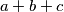 can obtain. The number
can obtain. The number 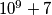 is prime.
is prime. 