Vrijeme: 18:09
Podijeljeni zajedno | Divided Together #3
Neka je 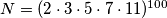 . Neka su
. Neka su 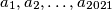 prirodni brojevi. Za
prirodni brojevi. Za  , neka je
, neka je 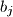 najveći zajednički djelitelj brojeva
najveći zajednički djelitelj brojeva  . Pretpostavimo da je
. Pretpostavimo da je 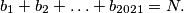 Neka je
Neka je  najmanja vrijednost koju može poprimiti izraz
najmanja vrijednost koju može poprimiti izraz 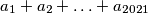 . Odredi
. Odredi 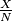 .
.
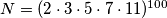 . Neka su
. Neka su 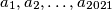 prirodni brojevi. Za
prirodni brojevi. Za  , neka je
, neka je 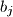 najveći zajednički djelitelj brojeva
najveći zajednički djelitelj brojeva  . Pretpostavimo da je
. Pretpostavimo da je 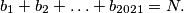 Neka je
Neka je  najmanja vrijednost koju može poprimiti izraz
najmanja vrijednost koju može poprimiti izraz 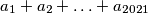 . Odredi
. Odredi 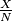 .
. Let 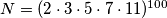 . Let
. Let 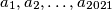 be positive integers. For
be positive integers. For  , let
, let 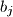 be the greatest common divisor of
be the greatest common divisor of  . Suppose that
. Suppose that 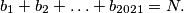 Let
Let  be the least possible value that
be the least possible value that 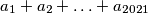 can obtain. Find
can obtain. Find 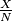 .
.
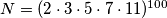 . Let
. Let 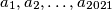 be positive integers. For
be positive integers. For  , let
, let 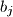 be the greatest common divisor of
be the greatest common divisor of  . Suppose that
. Suppose that 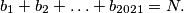 Let
Let  be the least possible value that
be the least possible value that 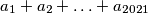 can obtain. Find
can obtain. Find 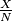 .
. 