Vrijeme: 12:49
Optimizacija ploče | Board Optimization #5
U svakom polju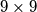 
ploče nalazi se žeton. U jednom potezu potrebno je izabrati dva susjedna žetona (čija polja dijele stranicu) i nakon toga se nasumično jedan od njih miče s ploče. Ako u ikojem trenutku postoji žeton koji je i dalje na ploči, a ima barem dva susjedna polja s kojih je maknut žeton, proces odmah prestaje. Koji je najveći broj poteza koji možemo osigurati da će se dogoditi, neovisno o tome koji od dva žetona je maknut u svakom potezu?
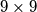ploče nalazi se žeton. U jednom potezu potrebno je izabrati dva susjedna žetona (čija polja dijele stranicu) i nakon toga se nasumično jedan od njih miče s ploče. Ako u ikojem trenutku postoji žeton koji je i dalje na ploči, a ima barem dva susjedna polja s kojih je maknut žeton, proces odmah prestaje. Koji je najveći broj poteza koji možemo osigurati da će se dogoditi, neovisno o tome koji od dva žetona je maknut u svakom potezu? There is a token in every cell of a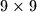 
board. A move consists of choosing two adjacent tokens (whose cells share a side) and after that one of them is randomly taken off the board. If at any moment there exists a token that is still on the board, but which has two adjacent cells from which a token was removed, the process stops immediately. What is the maximum possible number of moves that we can ensure will happen, regardless of which of the two tokens is chosen in each move?
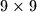board. A move consists of choosing two adjacent tokens (whose cells share a side) and after that one of them is randomly taken off the board. If at any moment there exists a token that is still on the board, but which has two adjacent cells from which a token was removed, the process stops immediately. What is the maximum possible number of moves that we can ensure will happen, regardless of which of the two tokens is chosen in each move?