Vrijeme: 18:09
Pošiljka iz Engleske | Package from England #4
Prvih  prirodnih brojeva podijeljeni su nasumično na padajući niz
prirodnih brojeva podijeljeni su nasumično na padajući niz  i rastući niz
i rastući niz 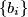 , pri čemu svaki ima
, pri čemu svaki ima  članova, a svaka podjela ima jednaku vjerojatnost da bude izabrana. Koliko iznosi očekivana vrijednost od
članova, a svaka podjela ima jednaku vjerojatnost da bude izabrana. Koliko iznosi očekivana vrijednost od 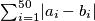 ?
?
 prirodnih brojeva podijeljeni su nasumično na padajući niz
prirodnih brojeva podijeljeni su nasumično na padajući niz  i rastući niz
i rastući niz 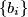 , pri čemu svaki ima
, pri čemu svaki ima  članova, a svaka podjela ima jednaku vjerojatnost da bude izabrana. Koliko iznosi očekivana vrijednost od
članova, a svaka podjela ima jednaku vjerojatnost da bude izabrana. Koliko iznosi očekivana vrijednost od 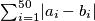 ?
? The first  positive integers are randomly split into a strictly decreasing sequence
positive integers are randomly split into a strictly decreasing sequence  and a strictly increasing sequence
and a strictly increasing sequence 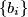 , each with
, each with  terms, where each such division has an equal probability of occuring. What is the expected value of
terms, where each such division has an equal probability of occuring. What is the expected value of 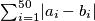 ?
?
 positive integers are randomly split into a strictly decreasing sequence
positive integers are randomly split into a strictly decreasing sequence  and a strictly increasing sequence
and a strictly increasing sequence 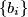 , each with
, each with  terms, where each such division has an equal probability of occuring. What is the expected value of
terms, where each such division has an equal probability of occuring. What is the expected value of 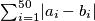 ?
? 