Odredi najmanji prirodni broj

takav da je
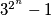
djeljivo s
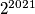
.
What is the smallest integer

such that
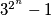
is divisible by
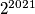
?
[lang=hr]
Odredi najmanji prirodni broj $n$ takav da je $3^{2^n} - 1$ djeljivo s $2^{2021}$.
[/lang]
[lang=en]
What is the smallest integer $n$ such that $3^{2^n} - 1$ is divisible by $2^{2021}$ ?
[/lang]