Vrijeme: 18:03
Bojanka | Coloring Book #4
Zadan je neusmjeren graf s  čvorova, označenih redom od
čvorova, označenih redom od  do
do  , pri čemu je
, pri čemu je 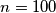 . Postoji brid između čvorova
. Postoji brid između čvorova  i
i 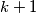 te između
te između 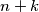 i
i  za sve prirodne brojeve
za sve prirodne brojeve 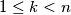 . Također, postoji brid između čvorova
. Također, postoji brid između čvorova  i
i  te između
te između 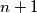 i
i  . Isto tako, bridovi povezuju
. Isto tako, bridovi povezuju  i
i 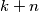 za sve prirodne brojeve
za sve prirodne brojeve 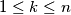 .
.
Na koliko načina možemo obojiti svaki čvor danog grafa u jednu od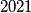 različitih boja tako da ne postoji brid čiji su vrhovi iste boje? Odgovor napišite modulo
različitih boja tako da ne postoji brid čiji su vrhovi iste boje? Odgovor napišite modulo 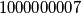 .
.
 čvorova, označenih redom od
čvorova, označenih redom od  do
do  , pri čemu je
, pri čemu je 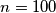 . Postoji brid između čvorova
. Postoji brid između čvorova  i
i 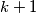 te između
te između 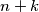 i
i  za sve prirodne brojeve
za sve prirodne brojeve 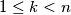 . Također, postoji brid između čvorova
. Također, postoji brid između čvorova  i
i  te između
te između 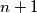 i
i  . Isto tako, bridovi povezuju
. Isto tako, bridovi povezuju  i
i 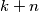 za sve prirodne brojeve
za sve prirodne brojeve 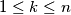 .
. Na koliko načina možemo obojiti svaki čvor danog grafa u jednu od
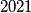 različitih boja tako da ne postoji brid čiji su vrhovi iste boje? Odgovor napišite modulo
različitih boja tako da ne postoji brid čiji su vrhovi iste boje? Odgovor napišite modulo 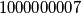 .
. An undirected graph with  nodes is given, where
nodes is given, where 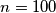 . The nodes are labeled with integers from
. The nodes are labeled with integers from  to
to  . There is an edge between nodes
. There is an edge between nodes  and
and 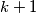 , and also between
, and also between 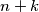 and
and  for every integer
for every integer 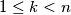 . Additionally, there is an edge between nodes
. Additionally, there is an edge between nodes  and
and  , and also between
, and also between 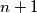 and
and  . Furthermore, there is an edge between
. Furthermore, there is an edge between  and
and 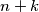 for every positive integer
for every positive integer 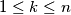 .
.
In how many ways can we color each node in one of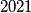 different colors such that there is no edge whose nodes are the same color? Write the answer modulo
different colors such that there is no edge whose nodes are the same color? Write the answer modulo 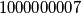 .
.
 nodes is given, where
nodes is given, where 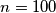 . The nodes are labeled with integers from
. The nodes are labeled with integers from  to
to  . There is an edge between nodes
. There is an edge between nodes  and
and 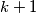 , and also between
, and also between 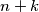 and
and  for every integer
for every integer 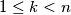 . Additionally, there is an edge between nodes
. Additionally, there is an edge between nodes  and
and  , and also between
, and also between 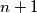 and
and  . Furthermore, there is an edge between
. Furthermore, there is an edge between  and
and 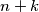 for every positive integer
for every positive integer 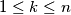 .
. In how many ways can we color each node in one of
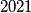 different colors such that there is no edge whose nodes are the same color? Write the answer modulo
different colors such that there is no edge whose nodes are the same color? Write the answer modulo 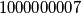 .
. 