Vrijeme: 18:03
Bojanka | Coloring Book #5
Zadan je neusmjeren graf s 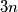 čvorova, označenih redom od
čvorova, označenih redom od  do
do 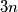 , pri čemu je
, pri čemu je 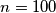 . Svi bridovi iz prethodnog zadatka u lancu također su prisutni i u ovom grafu. Dodatno, postoje i bridovi između
. Svi bridovi iz prethodnog zadatka u lancu također su prisutni i u ovom grafu. Dodatno, postoje i bridovi između 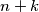 i
i 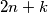 za sve prirodne brojeve
za sve prirodne brojeve 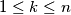 .
.
Na koliko načina možemo svakom bridu odrediti usmjerenje tako da ne postoji usmjereni ciklus? Odgovor napišite modulo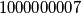 .
.
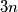 čvorova, označenih redom od
čvorova, označenih redom od  do
do 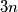 , pri čemu je
, pri čemu je 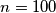 . Svi bridovi iz prethodnog zadatka u lancu također su prisutni i u ovom grafu. Dodatno, postoje i bridovi između
. Svi bridovi iz prethodnog zadatka u lancu također su prisutni i u ovom grafu. Dodatno, postoje i bridovi između 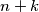 i
i 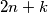 za sve prirodne brojeve
za sve prirodne brojeve 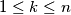 .
. Na koliko načina možemo svakom bridu odrediti usmjerenje tako da ne postoji usmjereni ciklus? Odgovor napišite modulo
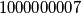 .
. An undirected graph with 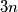 nodes is given, where
nodes is given, where 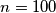 . The nodes are labeled with integers from
. The nodes are labeled with integers from  to
to 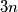 . All of the edges from the previous problem are also present in the graph given here. Additionally, there is an edge between the nodes
. All of the edges from the previous problem are also present in the graph given here. Additionally, there is an edge between the nodes 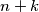 and
and 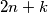 for every integer
for every integer 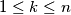 .
.
In how many ways can we assign a direction for each edge in such a way that there is no directed cycle in the graph? Write the answer modulo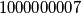 .
.
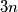 nodes is given, where
nodes is given, where 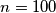 . The nodes are labeled with integers from
. The nodes are labeled with integers from  to
to 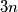 . All of the edges from the previous problem are also present in the graph given here. Additionally, there is an edge between the nodes
. All of the edges from the previous problem are also present in the graph given here. Additionally, there is an edge between the nodes 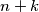 and
and 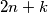 for every integer
for every integer 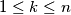 .
. In how many ways can we assign a direction for each edge in such a way that there is no directed cycle in the graph? Write the answer modulo
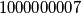 .
. 