Vrijeme: 18:03
Polinomi | Polynomials #4
Zadan je polinom 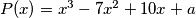 koji ima nultočke
koji ima nultočke  ,
, 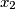 i
i 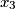 . Odredite vrijednost parametra
. Odredite vrijednost parametra  tako da je izraz
tako da je izraz 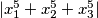 minimiziran. Moguće je pokazati da se odgovor može napisati u obliku
minimiziran. Moguće je pokazati da se odgovor može napisati u obliku 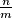 za prirodne brojeve
za prirodne brojeve  i
i  .
.
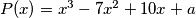 koji ima nultočke
koji ima nultočke  ,
, 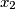 i
i 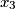 . Odredite vrijednost parametra
. Odredite vrijednost parametra  tako da je izraz
tako da je izraz 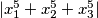 minimiziran. Moguće je pokazati da se odgovor može napisati u obliku
minimiziran. Moguće je pokazati da se odgovor može napisati u obliku 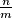 za prirodne brojeve
za prirodne brojeve  i
i  .
. The polynomial 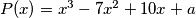 is given. It's roots are
is given. It's roots are  ,
, 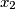 and
and 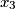 . Determine the value of the parameter
. Determine the value of the parameter  such that the expression
such that the expression 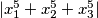 is minimized. It can be shown that the answer has the form of
is minimized. It can be shown that the answer has the form of 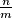 for positive integers
for positive integers  and
and  .
.
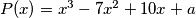 is given. It's roots are
is given. It's roots are  ,
, 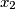 and
and 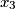 . Determine the value of the parameter
. Determine the value of the parameter  such that the expression
such that the expression 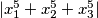 is minimized. It can be shown that the answer has the form of
is minimized. It can be shown that the answer has the form of 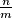 for positive integers
for positive integers  and
and  .
. 