Polinom

stupnja
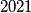
ima točno tri različite nultočke. Koliko najviše koeficijenta tog polinoma može iznositi

?
Polynomial

of degree
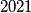
has exactly three different roots. What is the maximum number of zero coefficients that

can have?
[lang=hr]
Polinom $P(x)$ stupnja $2021$ ima točno tri različite nultočke. Koliko najviše koeficijenta tog polinoma može iznositi $0$?
[/lang]
[lang=en]
Polynomial $P(x)$ of degree $2021$ has exactly three different roots. What is the maximum number of zero coefficients that $P(x)$ can have?
[/lang]