Vrijeme: 18:07
Pa to je strašno | Well that's scary. #4
Neka je  prirodan broj i neka je
prirodan broj i neka je  najmanji prirodan broj tako da za svaki pozitivan prirodan broj
najmanji prirodan broj tako da za svaki pozitivan prirodan broj  , u bilo kojem podskupu od
, u bilo kojem podskupu od  elemenata od skupa
elemenata od skupa  postoji barem 3 po parovima relativno prosta broja.
postoji barem 3 po parovima relativno prosta broja.
Odredi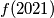 .
.
 prirodan broj i neka je
prirodan broj i neka je  najmanji prirodan broj tako da za svaki pozitivan prirodan broj
najmanji prirodan broj tako da za svaki pozitivan prirodan broj  , u bilo kojem podskupu od
, u bilo kojem podskupu od  elemenata od skupa
elemenata od skupa  postoji barem 3 po parovima relativno prosta broja.
postoji barem 3 po parovima relativno prosta broja. Odredi
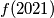 .
. Let  be a positive integer and let
be a positive integer and let  be the smallest number such that for every positive integer
be the smallest number such that for every positive integer  , in any subset of
, in any subset of  elements of the set
elements of the set  there exist 3 pairwise relatively prime numbers.
there exist 3 pairwise relatively prime numbers.
Determine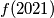 .
.
 be a positive integer and let
be a positive integer and let  be the smallest number such that for every positive integer
be the smallest number such that for every positive integer  , in any subset of
, in any subset of  elements of the set
elements of the set  there exist 3 pairwise relatively prime numbers.
there exist 3 pairwise relatively prime numbers. Determine
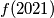 .
. 