Vrijeme: 18:03
Pa to je strašno | Well that's scary. #5
Za prirodan broj  , ako postoje prirodni brojevi
, ako postoje prirodni brojevi  ,
, ,
, i
i  takvi da je
takvi da je 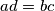 i da vrijedi:
i da vrijedi: 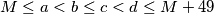 onda kažemo da je
onda kažemo da je  super broj, inače kažemo da je
super broj, inače kažemo da je  grozan broj. Odredi najveći 'super' broj i najmanji 'grozan' broj.
grozan broj. Odredi najveći 'super' broj i najmanji 'grozan' broj.
 , ako postoje prirodni brojevi
, ako postoje prirodni brojevi  ,
, ,
, i
i  takvi da je
takvi da je 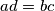 i da vrijedi:
i da vrijedi: 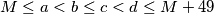 onda kažemo da je
onda kažemo da je  super broj, inače kažemo da je
super broj, inače kažemo da je  grozan broj. Odredi najveći 'super' broj i najmanji 'grozan' broj.
grozan broj. Odredi najveći 'super' broj i najmanji 'grozan' broj. For a positive integer  , if there exist positive integers
, if there exist positive integers  ,
, ,
, i
i  such that
such that 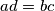 and also:
and also: 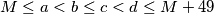 than we say that
than we say that  is 'superb' number, on the contrary we say that
is 'superb' number, on the contrary we say that  is a 'terrible' number. Determine the biggest 'superb' number and the smallest 'terrible' number.
is a 'terrible' number. Determine the biggest 'superb' number and the smallest 'terrible' number.
 , if there exist positive integers
, if there exist positive integers  ,
, ,
, i
i  such that
such that 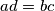 and also:
and also: 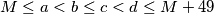 than we say that
than we say that  is 'superb' number, on the contrary we say that
is 'superb' number, on the contrary we say that  is a 'terrible' number. Determine the biggest 'superb' number and the smallest 'terrible' number.
is a 'terrible' number. Determine the biggest 'superb' number and the smallest 'terrible' number. 