Vrijeme: 18:09
Pa to je strašno | Well that's scary. #2
Za  definirajmo skupove
definirajmo skupove 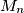 na sljedeći način:
na sljedeći način:
-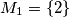
- za ,
, 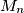 je najmanji skup koji sadrži
je najmanji skup koji sadrži 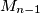 te koji sadrži sve proste faktore od
te koji sadrži sve proste faktore od 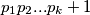 , za sve podskupove
, za sve podskupove 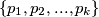 od
od 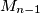
Definirajmo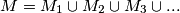 , te neka je
, te neka je 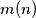 oznaka za
oznaka za  -ti po redu broj u
-ti po redu broj u  , a
, a 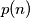 za
za  -ti po redu prost broj.
-ti po redu prost broj.
Odredi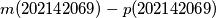 .
.
 definirajmo skupove
definirajmo skupove 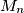 na sljedeći način:
na sljedeći način: -
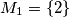
- za
 ,
, 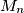 je najmanji skup koji sadrži
je najmanji skup koji sadrži 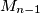 te koji sadrži sve proste faktore od
te koji sadrži sve proste faktore od 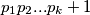 , za sve podskupove
, za sve podskupove 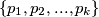 od
od 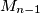
Definirajmo
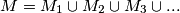 , te neka je
, te neka je 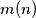 oznaka za
oznaka za  -ti po redu broj u
-ti po redu broj u  , a
, a 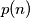 za
za  -ti po redu prost broj.
-ti po redu prost broj. Odredi
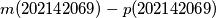 .
. For  define the set
define the set 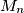 as follows:
as follows:
-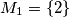
- for ,
, 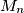 is the smallest set that contains
is the smallest set that contains 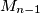 and that also contains all of the factors of
and that also contains all of the factors of 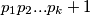 for all subsets
for all subsets 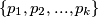 of
of 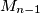 .
.
Define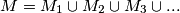 and let
and let 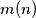 denote the
denote the  -th number in the set
-th number in the set  (when ordered by value), and let
(when ordered by value), and let 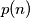 denote the
denote the  -th prime.
-th prime.
Calculate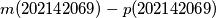 .
.
 define the set
define the set 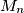 as follows:
as follows: -
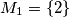
- for
 ,
, 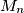 is the smallest set that contains
is the smallest set that contains 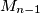 and that also contains all of the factors of
and that also contains all of the factors of 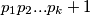 for all subsets
for all subsets 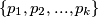 of
of 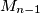 .
. Define
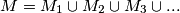 and let
and let 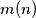 denote the
denote the  -th number in the set
-th number in the set  (when ordered by value), and let
(when ordered by value), and let 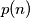 denote the
denote the  -th prime.
-th prime. Calculate
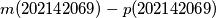 .
. 