Neka je

prirodan broj kojem je zapis u decimalnom sustavu dan sa
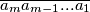
. Gdje je svaki

,
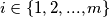
prirodan broj.
Odredi najveći

za koji vrijedi:
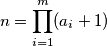
.
Let

be positive integer with the decimal representation
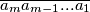
. where every

,
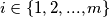
is a positive integer.
What is the maximum

for which the following holds:
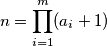
.
[lang=hr]
Neka je $n$ prirodan broj kojem je zapis u decimalnom sustavu dan sa $\overline{a_ma_{m-1}...a_1}$. Gdje je svaki $a_i$, $i \in \{1,2,...,m\}$ prirodan broj.
\\Odredi najveći $n$ za koji vrijedi: $$n=\prod_{i=1}^{m}(a_i + 1)$$.
[/lang]
[lang=en]
Let $n$ be positive integer with the decimal representation $\overline{a_ma_{m-1}...a_1}$. where every $a_i$, $i \in \{1,2,...,m\}$ is a positive integer.
\\What is the maximum $n$ for which the following holds: $$n=\prod_{i=1}^{m}(a_i + 1)$$.
[/lang]