Vrijeme: 18:03
Pa to je strašno | Well that's scary. #3
Neka je 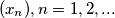 niz definiran sa
niz definiran sa 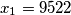 i
i 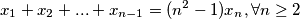 Neka je niz
Neka je niz 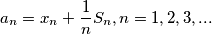 gdje je
gdje je 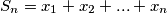 . Odredi sve
. Odredi sve  za koje je
za koje je  potpuni kvadrat prirodnog broja. Ako je više odgovora napišite ih uzlazno.
potpuni kvadrat prirodnog broja. Ako je više odgovora napišite ih uzlazno.
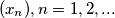 niz definiran sa
niz definiran sa 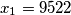 i
i 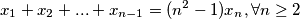 Neka je niz
Neka je niz 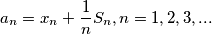 gdje je
gdje je 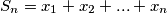 . Odredi sve
. Odredi sve  za koje je
za koje je  potpuni kvadrat prirodnog broja. Ako je više odgovora napišite ih uzlazno.
potpuni kvadrat prirodnog broja. Ako je više odgovora napišite ih uzlazno. Let 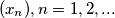 be a sequence defined by
be a sequence defined by 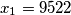 and
and 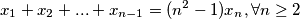 Let the sequence
Let the sequence 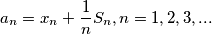 where
where 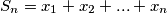 . Determine the values of
. Determine the values of  for which the terms of the sequence
for which the terms of the sequence  are perfect squares of an integer. If there is more than one answer, write them in ascending order.
are perfect squares of an integer. If there is more than one answer, write them in ascending order.
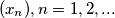 be a sequence defined by
be a sequence defined by 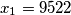 and
and 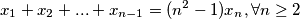 Let the sequence
Let the sequence 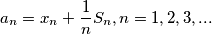 where
where 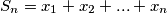 . Determine the values of
. Determine the values of  for which the terms of the sequence
for which the terms of the sequence  are perfect squares of an integer. If there is more than one answer, write them in ascending order.
are perfect squares of an integer. If there is more than one answer, write them in ascending order. 