Zadan je polinom
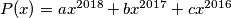
, pri čemu su koeficijenti

,

i

manji ili jednaki od
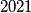
. Vrijedi
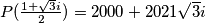
. Koliko iznosi
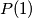
?
The polynomial
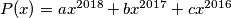
is given, where each of the coefficients

,

and

is less than or equal to
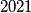
, and
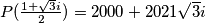
. Find the value of
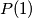
.
[lang=hr]
Zadan je polinom $P(x) = a x^{2018} + b x^{2017} + c x^{2016}$, pri čemu su koeficijenti $a$, $b$ i $c$ manji ili jednaki od $2021$. Vrijedi $P(\frac{1 + \sqrt{3}i}{2}) = 2000 + 2021\sqrt{3}i$. Koliko iznosi $P(1)$?
[/lang]
[lang=en]
The polynomial $P(x) = a x^{2018} + b x^{2017} + c x^{2016}$ is given, where each of the coefficients $a$, $b$ and $c$ is less than or equal to $2021$, and $P(\frac{1 + \sqrt{3}i}{2}) = 2000 + 2021\sqrt{3}i$. Find the value of $P(1)$.
[/lang]