Odredi najmanji
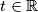
takav da za sve
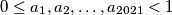
koji zadovoljavaju
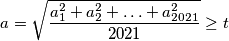
vrijedi
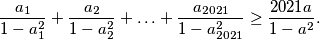
Determine the least
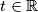
such that for all
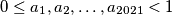
that satisfy
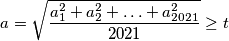
we have
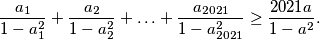
[lang=hr]
Odredi najmanji \(t \in \mathbb{R}\) takav da za sve \(0 \leq a_1,a_2,\ldots ,a_{2021} <1\) koji zadovoljavaju
\[a = \sqrt{\frac{a_1^2+a_2^2+\ldots+a_{2021}^2}{2021}} \geq t\]
vrijedi
\[\frac{a_1}{1-a_1^2} + \frac{a_2}{1-a_2^2} + \ldots +\frac{a_{2021}}{1-a_{2021}^2} \geq \frac{2021a}{1-a^2}.\]
[/lang]
[lang=en]
Determine the least \(t \in \mathbb{R}\) such that for all \(0\leq a_1,a_2,\ldots ,a_{2021}<1\) that satisfy
\[a = \sqrt{\frac{a_1^2+a_2^2+\ldots+a_{2021}^2}{2021}} \geq t\]
we have
\[\frac{a_1}{1-a_1^2} + \frac{a_2}{1-a_2^2} + \ldots +\frac{a_{2021}}{1-a_{2021}^2} \geq \frac{2021a}{1-a^2}.\]
[/lang]