Odredi najmanji
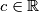
takav da za sve
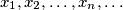
takve da je
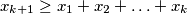
za svaki
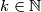
, nejednakost
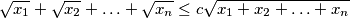
vrijedi za svaki
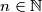
.
Determine the smallest
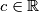
such that for all
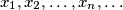
that satisfy
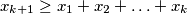
for all
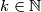
, the inequality
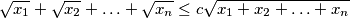
holds for all
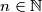
.
[lang=hr]
Odredi najmanji \(c \in \mathbb{R}\) takav da za sve \(x_1,x_2,\ldots ,x_n, \ldots\) takve da je \(x_{k+1}\geq x_1+x_2+\ldots +x_k\) za svaki \(k \in \mathbb{N}\), nejednakost
\[\sqrt{x_1}+\sqrt{x_2}+\ldots+\sqrt{x_n} \leq c\sqrt{x_1+x_2+\ldots+x_n}\]
vrijedi za svaki \(n \in \mathbb{N}\).\\
[/lang]
[lang=en]
Determine the smallest \(c \in \mathbb{R}\) such that for all \(x_1,x_2,\ldots ,x_n,\ldots \) that satisfy \(x_{k+1}\geq x_1+x_2+\ldots +x_k\) for all \(k \in \mathbb{N}\), the inequality
\[\sqrt{x_1}+\sqrt{x_2}+\ldots+\sqrt{x_n} \leq c\sqrt{x_1+x_2+\ldots+x_n}\]
holds for all \(n \in \mathbb{N}\).
[/lang]