Vrijeme: 17:58
Nizozemski lanac | Dutch chain #5
Kees računa umnožak svih znamenki svakog  -znamenkastog broja, a zatim zbraja sve umnoške kako bi dobio
-znamenkastog broja, a zatim zbraja sve umnoške kako bi dobio  . Budući da je
. Budući da je  prilično velik broj, odlučio je rezultat
prilično velik broj, odlučio je rezultat  zapisati kao
zapisati kao  modulo svog omiljenog prostog broja,
modulo svog omiljenog prostog broja, 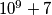 . Odredi
. Odredi  takav da je
takav da je 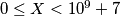 and
and 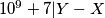 .
.
 -znamenkastog broja, a zatim zbraja sve umnoške kako bi dobio
-znamenkastog broja, a zatim zbraja sve umnoške kako bi dobio  . Budući da je
. Budući da je  prilično velik broj, odlučio je rezultat
prilično velik broj, odlučio je rezultat  zapisati kao
zapisati kao  modulo svog omiljenog prostog broja,
modulo svog omiljenog prostog broja, 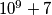 . Odredi
. Odredi  takav da je
takav da je 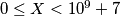 and
and 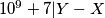 .
. Kees computes the product of the digits of every  -digit number, then he adds all products together to make the number
-digit number, then he adds all products together to make the number  . Since
. Since  is quite a big number, he decides to reduce it modulo his favourite prime
is quite a big number, he decides to reduce it modulo his favourite prime 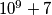 to
to  . Output the number
. Output the number  such that
such that 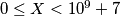 i
i 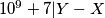 .
.
 -digit number, then he adds all products together to make the number
-digit number, then he adds all products together to make the number  . Since
. Since  is quite a big number, he decides to reduce it modulo his favourite prime
is quite a big number, he decides to reduce it modulo his favourite prime 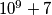 to
to  . Output the number
. Output the number  such that
such that 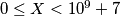 i
i 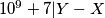 .
. 