Vrijeme: 18:00
Najružniji lanac | The Ugliest Chain #2
Sljedeći zadatak kojemu nedostaje rješenje uključuje kvadratni polinom s realnim koeficijentima,  , takav da vrijedi
, takav da vrijedi 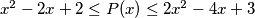 za sve realne
za sve realne  . Pretpostavimo da je
. Pretpostavimo da je 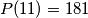 . Koliko je
. Koliko je 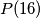 ?
?
 , takav da vrijedi
, takav da vrijedi 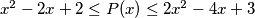 za sve realne
za sve realne  . Pretpostavimo da je
. Pretpostavimo da je 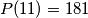 . Koliko je
. Koliko je 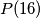 ?
? The following problem that misses a solution includes a quadratic polynomial with real coefficients  such that
such that 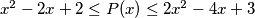 holds true for all real
holds true for all real  . Suppose
. Suppose 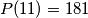 . Determine
. Determine 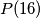 .
.
 such that
such that 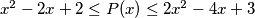 holds true for all real
holds true for all real  . Suppose
. Suppose 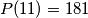 . Determine
. Determine 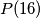 .
. 