Vrijeme: 18:00
Najružniji lanac | The Ugliest Chain #1
Slavomir je od malena bio neobično dijete, a to se nije promijenilo ni kada je zavolio matematičke zadatke. Naime, Slavomirovi omiljeni zadaci bili su oni koji uključuju najružnije izraze. Štoviše, Slavomir je toliko volio ružne izraze da je svoje omiljene uvrstio u osobnu kolekciju. Skupio je mnogo zadataka, ali nažalost Slavomir nije ni približno dobar matematičar koliko je spretan kao kolekcionar. Pomozite Slavomiru da upotpuni svoju zbirku ružnih zadataka lijepim (ili ne) rješenjima!
Za svaki uređeni par realnih brojeva koji zadovoljava
koji zadovoljava 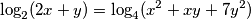 postoji realni broj
postoji realni broj  takav da vrijedi
takav da vrijedi 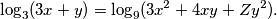
Koliki je umnožak svih mogućih ?
?
Za svaki uređeni par realnih brojeva
 koji zadovoljava
koji zadovoljava 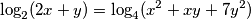 postoji realni broj
postoji realni broj  takav da vrijedi
takav da vrijedi 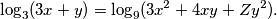
Koliki je umnožak svih mogućih
 ?
? From young age, Slavomir has been one unusual child, a fact that hasn't changed when he fell in love with math problems. Slavomir's favourite problems are those that include the ugliest expressions. Moreover, Slavomir likes ugly expressions so much that he decided to make a personal collection. He's collected many problems. Unfortunately Slavomir isn't nearly as good a mathematician as he is a collector. Help him complete his collection of ugly problems with nice (or not) solutions.
For every ordered pair of real numbers that satisfy
that satisfy 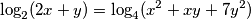 there exists a real number
there exists a real number  such that
such that 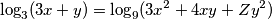 hold true. Calculate the product of all possible values of
hold true. Calculate the product of all possible values of  .
.
For every ordered pair of real numbers
 that satisfy
that satisfy 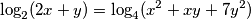 there exists a real number
there exists a real number  such that
such that 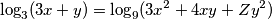 hold true. Calculate the product of all possible values of
hold true. Calculate the product of all possible values of  .
. 