Vrijeme: 18:00
Najružniji lanac | The Ugliest Chain #3
Miroslav nikako ne može shvatiti opsesiju svog prijatelja, ali kad god naiđe na neki zadatak od kojeg mu se izokrene želudac sjeti se Slavomirove kolekcije pa zadatak ljubazno proslijedi našem kolekcionaru. Evo jednog zadatka na koji je Miroslav nedavno naišao:
Neka je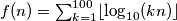 za sve prirodni
za sve prirodni  . Koji je najveći
. Koji je najveći  takav da je
takav da je 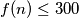 ?
?
Neka je
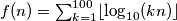 za sve prirodni
za sve prirodni  . Koji je najveći
. Koji je najveći  takav da je
takav da je 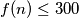 ?
? Miroslav doesn't get his firend's opsession, but anytime he stumbles upon a problem that makes him sick he remembers Slavomir's collection so he kindly sends the problem to our collector. Here is one problem that Miroslav recently found:
Let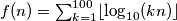 for all positive integers
for all positive integers  . Determine the greatest
. Determine the greatest  such that
such that 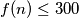 ?
?
Let
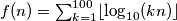 for all positive integers
for all positive integers  . Determine the greatest
. Determine the greatest  such that
such that 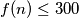 ?
? 