Vrijeme: 17:59
Najružniji lanac | The Ugliest Chain #4
Kruna Slavomirove kolekcije ipak je jedan zadatak koji je vidio još dok nije znao reći ni kosinus (Je li to izvor njegovih čudnih zanimacija? Tko bi znao...)
Neka je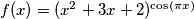 . Pronađi zbroj svih prirodnih brojeva
. Pronađi zbroj svih prirodnih brojeva  za koje je
za koje je 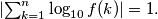
Neka je
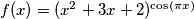 . Pronađi zbroj svih prirodnih brojeva
. Pronađi zbroj svih prirodnih brojeva  za koje je
za koje je 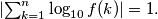
Crown jewel of Slavomir's collection is a problem that he saw long time ago, when he couldn't yet even spell cos (Might this be the source of his strange hobby? Who's to say...)
Let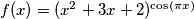 . Find the sum of all positive integers
. Find the sum of all positive integers  for which
for which 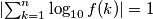 holds true.
holds true.
Let
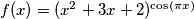 . Find the sum of all positive integers
. Find the sum of all positive integers  for which
for which 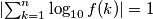 holds true.
holds true. 