Neka su

i

prirodni brojevi takvi da
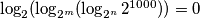
. Koliki je zbroj svih mogućih vrijednosti broja
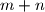
?
Let

and

be two positive integers that satisfy the equation
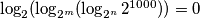
. Find the sum of all possible values of

.
[lang=hr]
Neka su $m$ i $n$ prirodni brojevi takvi da $\log_2(\log_{2^m}(\log_{2^n} 2^{1000})) = 0$. Koliki je zbroj svih mogućih vrijednosti broja $m + n$?
[/lang]
\\ \\
[lang=en]
Let $m$ and $n$ be two positive integers that satisfy the equation $\log_2(\log_{2^m}(\log_{2^n} 2^{1000})) = 0$. Find the sum of all possible values of $m +n$.
[/lang]